History’s most famous scientist, Albert Einstein, is believed to have said:
“Compound interest is the eighth wonder of the world.
He who understands it, earns it; he who doesn’t, pays it.”
Compound interest (also known as compounding interest) is interest calculated on the initial principle, plus all the interest earned on all the previous periods of a deposit or loan. Essentially, it is interest earned upon interest and the original principle. The rate at which it grows increases in speed as the interest earned is reinvested. This is the magic of compound interest, as opposed to simple interestwhich is calculated only on the original principle.
The rate at which compound interest will grow is dependent on the frequency of the compounding periods. For example, take a $10,000 deposit, compounded annually at 12% interest. After ten years, it will have amassed a total value of $31,058.48. Compare that to the same $10,000 deposit, compounded bi-annually (i.e. every six months) at 6% interest will amass a total value of $32,071.35 over the same ten-year period – a more than $1,000 difference. The more frequent the compounding periods, the faster your money will grow.
A deposit of $10,000 calculated annually at 12% simple interest over a ten-year period, will yield a total value of only $22,000 – less than $9,000 compared to compounding interest.
If you were to add $100 each month to the initial $10,000 deposit compounded annually at 12% interest. After ten years, it will have amassed a total value of $53,462.07. Over a ten-year period, you will have added a further $22,403.59 to your final sum. That is, a further $10,000 from compound interest, simply by adding an extra $100 to your initial investment each month.
| Year | Investment | Interest | Balance |
| 1 | $11,200.00 | $1,276.66 | $12,476.65 |
| 2 | $1,200.00 | $1,573.85 | $15,250.50 |
| 3 | $1,200.00 | $1,906.73 | $18,357.21 |
| 4 | $1,200.00 | $2,279.52 | $21,836.72 |
| 5 | $1,200.00 | $2,697.06 | $25,733.78 |
| 6 | $1,200.00 | $3,164.70 | $30,098.48 |
| 7 | $1,200.00 | $3,688.47 | $34,986.95 |
| 8 | $1,200.00 | $4,275.08 | $40,462.03 |
| 9 | $1,200.00 | $4,932.09 | $46,594.13 |
| 10 | $1,200.00 | $5,667.95 | $53,462.07 |
| Totals | $22,000.00 | $31,462.07 | $53,462.07 |
This is the miracle of compound interest, because the effect of creating interest-upon-interest from the original principle generates increasingly positive returns.
To take advantage of compounding interest and to build your portfolio, consider the two following examples of investing and trading on the global financial markets.
The S&P 500 Index, or S&P, is an index created by Standard & Poor’s, a company established in 1860, to provide financial information, analysis and valuations of five hundred large companies in America.
Since 1957, the S&P 500 has grown annually at an average rate of 8%. An investment of $10,000 in the S&P 500 over a ten-year period would have yielded a total sum of $21,589.25
Compare that to Warren Buffett, regarded as one of the world’s most successful investors, who has consistently beat the market with an average annual return of 21% over fifty years.
An investment of $10,000 compounding at 21% over a ten-year period would have yielded a total sum of $67.275.00. Relatively small changes in the amount of interest earned has dramatic effects on the overall returns, as does the length of time the deposit is compounding.
To put this into perspective a $1,000 investment in the S&P 500 fifty years ago compounding annually at a rate of 8%, would be worth $46,901.01
A $1,000 investment grown at a rate of 21% for fifty years would be worth $13,780,612.34
| Year | Investment | Interest | Balance |
| 1 | $1,000.00 | $210.00 | $1,210.00 |
| 2 | $0.00 | $254.09 | $1,464.10 |
| 3 | $0.00 | $307.47 | $1,771.56 |
| 4 | $0.00 | $372.03 | $2,143.59 |
| 5 | $0.00 | $450.15 | $2,593.74 |
| 6 | $0.00 | $544.69 | $3,138.43 |
| 7 | $0.00 | $659.07 | $3,797.50 |
| 8 | $0.00 | $797.47 | $4,594.97 |
| 9 | $0.00 | $964.94 | $5,559.92 |
| 10 | $0.00 | $1,167.58 | $6,727.50 |
| 2030 | $0.00 | $1,412.79 | $8,140.27 |
| 2031 | $0.00 | $1,709.46 | $9,849.73 |
| 2032 | $0.00 | $2,068.42 | $11,918.18 |
| 2033 | $0.00 | $2,502.83 | $14,420.99 |
| 2034 | $0.00 | $3,028.41 | $17,449.40 |
| 2035 | $0.00 | $3,664.38 | $21,113.78 |
| 2036 | $0.00 | $4,433.88 | $25,547.67 |
| 2037 | $0.00 | $5,365.02 | $30,912.68 |
| 2038 | $0.00 | $6,491.66 | $37,404.34 |
| 2039 | $0.00 | $7,854.89 | $45,259.26 |
| 2040 | $0.00 | $9,504.46 | $54,763.70 |
| 2041 | $0.00 | $11,500.37 | $66,264.08 |
| 2042 | $0.00 | $13,915.46 | $80,179.53 |
| 2043 | $0.00 | $16,837.71 | $97,017.23 |
| 2044 | $0.00 | $20,373.62 | $117,390.85 |
| 2045 | $0.00 | $24,652.08 | $142,042.93 |
| 2046 | $0.00 | $29,829.01 | $171,871.95 |
| 2047 | $0.00 | $36,093.11 | $207,965.06 |
| 2048 | $0.00 | $43,672.66 | $251,637.72 |
| 2049 | $0.00 | $52,843.92 | $304,481.64 |
| 2050 | $0.00 | $63,941.16 | $368,422.78 |
| 2051 | $0.00 | $77,368.78 | $445,791.57 |
| 2052 | $0.00 | $93,616.23 | $539,407.80 |
| 2053 | $0.00 | $113,275.63 | $652,683.44 |
| 2054 | $0.00 | $137,063.53 | $789,746.96 |
| 2055 | $0.00 | $165,846.87 | $955,593.82 |
| 2056 | $0.00 | $200,674.70 | $1,156,268.52 |
| 2057 | $0.00 | $242,816.39 | $1,399,084.91 |
| 2058 | $0.00 | $293,807.83 | $1,692,892.74 |
| 2059 | $0.00 | $355,507.47 | $2,048,400.21 |
| 2060 | $0.00 | $430,164.03 | $2,478,564.26 |
| 2061 | $0.00 | $520,498.49 | $2,999,062.75 |
| 2062 | $0.00 | $629,803.21 | $3,628,865.93 |
| 2063 | $0.00 | $762,061.85 | $4,390,927.78 |
| 2064 | $0.00 | $922,094.83 | $5,313,022.61 |
| 2065 | $0.00 | $1,115,734.74 | $6,428,757.36 |
| 2066 | $0.00 | $1,350,039.03 | $7,778,796.41 |
| 2067 | $0.00 | $1,633,547.27 | $9,412,343.65 |
| 2068 | $0.00 | $1,976,592.16 | $11,388,935.82 |
| 2069 | $0.00 | $2,391,676.52 | $13,780,612.34 |
| Totals | $1,000.00 | $13,779,612.34 | $13,780,612.34 |
Seemingly small changes have a big effect on the end result, when the effect of compounding is taken into account.
To calculate compound interest, multiply the original principle by one plus the annual rate of interest, raised to the total number of compounding periods. The initial deposit is then subtracted from the sum to reveal the total interest earned over that period.
The formula for calculating compound interest is:
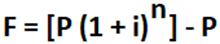
Where F is the future interest earned, P is the original principle, i is the annual interest rate expressed as a percent, and n is the total number of compounding periods.
To convert the interest rate to a decimal percentage, take the percent number and move the decimal point two places to the left, the effect of which is to divide the number by a hundred. Thus, an interest rate of 12% become 0.12, and an interest rate of 3% become 0.03.
Let’s take a five-year loan of $2,000 and calculate the compounding interest at an annual rate of 7%.
[2,000 (1 + 0.07) ^5] – 2,000 = $2,805.10
We can change this formula around to calculate the original principle required if we want to accumulate a particular sum of money by a future date:
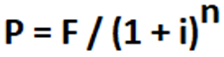
If we take our same example, to accumulate a sum of $2,805.10 within a five-year period using compounding interest, we will need an initial principle of at least $2,000.
2,000 = $2,805.10 / ([2,000 (1 + 0.07)^5])
You can also calculate the interest rate ‘i’ if you know the initial principle ‘P’, the accumulated future value ‘F’, and the number of compounding periods ‘n’.
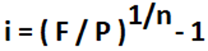
Again, using our above example, to calculate the interest rate ‘i’, for a five-year loan of $2,000 and accumulate a sum of $2,805 the interest will need to be at least 7%.
0.07 = (2,805.10 / 2,000) ^(1/5) – 1
0.07 x 100 = 7%
To calculate the number of compounding periods required to accumulate a sum of $2,805 from an initial principle of $2,000 at a rate of 7% interest, the logarithm function can be used.
Many spreadsheets and hand-held calculators have built-in functions for assisting in these calculations.
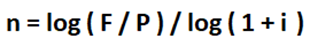
Thus, using our above example:
5.0 = log (2,805.10 / 2,000) / log (1 + 0.07)
Therefore, at least 5 compounding periods would be required to accumulate a sum of $2,805 from an initial principle of $2,000 at a rate of 7% interest.
As stated above, the number of compounding periods can significantly influence your final accumulated sum. Interest on bank savings accounts are commonly compounded daily. Alternatively, interest on CDs can be compounded daily, monthly or semi-annually. The interest on home mortgage loans, home equity loans, personal business loans or credit card accounts are usually compounded monthly.
Variations in the timeframe can also occur where the accrued interest is actually credited to the existing balance. Interest on an account may be compounded daily but only credited monthly. It is only when the interest is actually credited (i.e. added to the existing balance), that it begins to earn additional interest in the account.
The more frequent the compounding periods, the more compound interest and the longer the time can benefit your savings; however, if you are a borrower, the opposite is true.
